Autonomous Learning System ModelWe swim in a stream of information. How we relate to this information defines how we perceive ourselves and determines how we act. We filter, process, incorporate, evaluate, and direct our search for additional information based on its perceived utility. We have free will yet we respond to new information in a characteristic manner.
In the frequency domain, high information rates correspond to high frequencies while lower frequencies carry fundamental information content by which the more discrete high frequency information quanta are biased. In this setting, information is processed through filters that are characterized by relative passband and gain which together determine the spectrum of information output through the filter. Since this method of understanding information flows is common in the communication field, let me propose the following model of the individual as an autonomous learning system:

Cognition is the state of the structure of the mind which results from the characteristic processing of information over time. In this way useful information is encoded and stored for future reference. The state of cognition is constantly being acted upon by the filtered information stream which in turn acts through the evaluation of that input to condition incoming information streams. Cognition directs how the individual filters are adaptively tuned.
The prefilter is adjusted to select those sources of information that are perceived to be of greatest utility in our environment and we act on that environment ourselves through the filtered cognitive output. The system reaches an optimal stability point when all filters are adjusted for the maximal encoding of useful information into the cognitive structure. It is not necessary for the stability point to be optimal in this regard. All stability points are representative of a characteristic response of the individual.
Ideally, the best description of the character of the individual would be achieved by measuring the cognitive state directly. One method that attempts to do this is to query the individual on various issues in the context of known demographics and to make inferences based on these observations. The interpretation of the responses is necessarily convoluted when the context of the environmental information changes at a rate near to or within the time constant of cognitive adaptation.
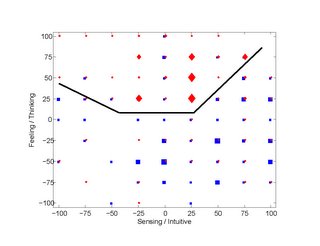
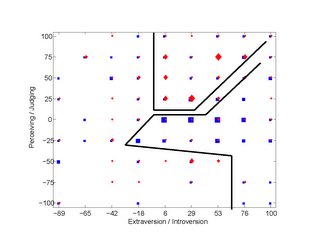
Another method to make inferences of the characteristic that is complementary to the method described above is to presume that the individual system operates at a stability point well described by the matching of the filters and then to measure the filters. We would like to investigate the potential of this approach through the measurement of ensembles of filter measurements in the social domain and the characteristic political affiliation decision in the context of the US two-party system.
The Myers-Briggs Information ModelThe commonly used
Myers-Briggs personality inventory is largely compatible to the measurement of the individual processing filters. The extroversion/introversion focus dimension is a combined description of the prefilter and output filter in the direct social contact domain. Note that this is a bit restrictive for our investigation as much if not the majority of political intercourse is indirect. Nonetheless, it is of interest to include this dimension in the analysis as it may yield insights into the stability of operating points which are also a function of the filters internal to the primary processing loop.
The focus dimension is measured by the questions:
(All questions come from the Humanmetrics test that was used in the study)
1. You feel at ease in a crowd
2. You rapidly get involved in social life at a new workplace
3. You spend your leisure time actively socializing with a group of people, attending parties, shopping, etc.
4. Direct-contact group discussions stimulate you and give you energy
5. The more people you speak to, the better you feel
6. You are usually the first to react to a sudden event: the telephone ringing or unexpected question
7. It is easy for you to communicate in social situations
8. You enjoy having a wide circle of acquaintances
9. You enjoy being at the center of events in which other people are directly involved
and
10. You get pleasure from solitary walks
11. After prolonged socializing you feel you need to get away and be alone
12. You prefer to spend your leisure time alone, within a narrow circle of friends or relaxing in a tranquil family atmosphere
13. You are able to cut yourself off from the bustle of everyday life
14. You are more of a listener than a speaker
15. You prefer meeting in small groups to interaction with lots of people
16. You usually place yourself nearer to the side than in the center of the room
17. You prefer to isolate yourself from outside noises
18. You find it difficult to speak loudly
There are two measurements of the primary loop input filter. The Myers-Briggs processing dimension of intuition/sensing is a measurement of unstructured information capacity of the input channel proportionate to the information encoded in the cognition. It is roughly analogous to the gain of the input filter relative to the degree of cognitive structure. The questions which measure this dimension are:
19. As a rule, current preoccupations worry you more than your future plans
20. You tend to rely on your experience rather than on theoretical alternatives
21. You prefer to act immediately rather than speculate about various options
22. Your desk, workbench etc. is usually neat and orderly
23. You have difficulty understanding the notion of "an approximate decision"
24. It's essential for you to try things with your own hands
25. When solving a problem you would rather follow a familiar approach than seek a new one
26. When considering a situation you pay more attention to the current situation and less to a possible sequence of events
27. You feel more comfortable sticking to conventional ways
28. You easily see the general principle behind specific occurrences
and
29. You are always looking for opportunities
30. You often spend time thinking of how things could be improved
31. You easily perceive various ways in which events could develop
32. You are more interested in a general idea than in the details of its realization
33. You easily understand new theoretical principles
34. You often think about the mankind and its destiny
35. You are more inclined to experiment than to follow familiar approaches
36. You are eager to know how things work
The passband of the input filter is described by the decision making feeling/thinking dimension. Note that 'feeling' is not simply a visceral response, but is also an efficient method of understanding thematic information. For example, consider the wonderful work of
John Sovjani. The information of the paintings displayed on the computer screen is actually a large but finite number of bits. Therefore, it is possible to develop a computer program that would describe the finite relations of the combinations of one or a group of pixels to the others. While this computer program might finally produce a set of essential relations that describes "Serenity", the encoding would almost definitely not be as tractable or useful as a brief observation of this work by a human. Thus it would be a precipitous conclusion to imply that the low frequency passband of feeling necessarily results in an inefficient encoding of complex social information.
The questions that relate to the decision making dimension are:
37. You find it difficult to talk about your feelings
38. It's difficult to get you excited or make you lose your temper
39. You trust reason rather than feelings
40. You value justice higher than mercy
41. You think that almost everything can be analyzed
42. Objective criticism is always useful in any activity
43. You tend to be unbiased even if this might endanger your good relations with people
44. You try to stand firmly by your principles
45. You consider the scientific approach to be the best
and
46. You tend to sympathize with other people
47. You are easily affected by strong emotions
48. You readily help people while asking nothing in return
49. You willingly involve yourself in matters which engage your sympathies
50. You feel involved when watching TV soaps
51. You easily empathize with the concerns of other people
52. Your actions are frequently influenced by emotions
53. You feel that the world is founded on compassion
54. In a debate, you strive to achieve mutual agreement
Finally, the filter which passes the cognitive output in order to direct the search and evaluation of new information is described by the organizing judging/perceiving dimension of the Myers-Briggs. At the judging end of the dimension the search and evaluation is more finely focused on propositions that would either confirm or deny the future utility of the present cognitive structure. Judging seeks to simplify the encoding of the input stream by clarifying the limits and sufficiency of the present encoding of the cognitive structure. Perceiving is an emphasis on exploring and seeking previously unencoded information in the input stream. The questions which relate to this dimension are:
55. You do your best to complete a task on time
56. It is in your nature to assume responsibility
57. You usually plan your actions in advance
58. You like to keep a check on how things are progressing
59. You take pleasure in putting things in order
60. You are consistent in your habits
61. You are almost never late for your appointments
62. You know how to put every minute of your time to good purpose
63. You like giving instructions
and
64. You are inclined to rely more on improvisation than on careful planning
65. Deadlines seem to you to be of relative rather than absolute importance
66. You think that everything in the world is relative
67. A thirst for adventure is something close to your heart
68. The process of searching for solution is more important to you than the solution itself
69. You avoid being bound by obligations
70. You often do jobs in a hurry
71. You believe the best decision is one which can be easily changed
72. Strict observance of the established rules is likely to prevent attaining a good outcome